卡方检验(Chi-Square Test)是一种用于检验观察数据与理论预期之间差异是否显著的统计方法。在医学研究中,卡方检验特别适用于分析分类数据,例如疾病的发病率、治疗效果以及不同因素之间的关系。
一、卡方检验的原理
卡方检验用于判断观察到的频数与预期频数之间的差异是否显著。其基本假设是:观察到的分布与预期分布无显著差异,即变量之间没有关联。卡方统计量的基本公式为:


自由度df=(行数-1)(列数-1)
二、四格表(2×2表)的结构
四格表卡方检验基于一个二维表格,也称为四格表。表格中的行和列分别代表两个分类变量。例如,行可以代表男性和女性,列可以代表吸烟和不吸烟。表格中的每个单元格代表两个变量的交叉部分,例如男性吸烟者的数量。四格表卡方检验的目的是确定这些变量之间是否存在关联,如果存在关联,则表示两个变量之间有统计学上的显著性关系。
四格表,也称为2×2表,是卡方检验中最常用的数据格式。其结构如下:
| 事件A | 非事件A | 合计 | |
|---|---|---|---|
| 事件B | a | b | a+b |
| 非事件B | c | d | c+d |
| 合计 | a+c | b+d | N |
• 事件A 和 事件B 是两个分类变量。
• a, b, c, d 是不同组合的观察频数。
• N 是总样本量。
三、四格表专用公式
1.专用公式 N≥40 且T≥5
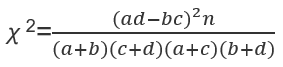
2.连续性矫正公式 N≥40 且1≤T<5
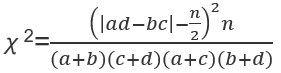
四、医学应用实例
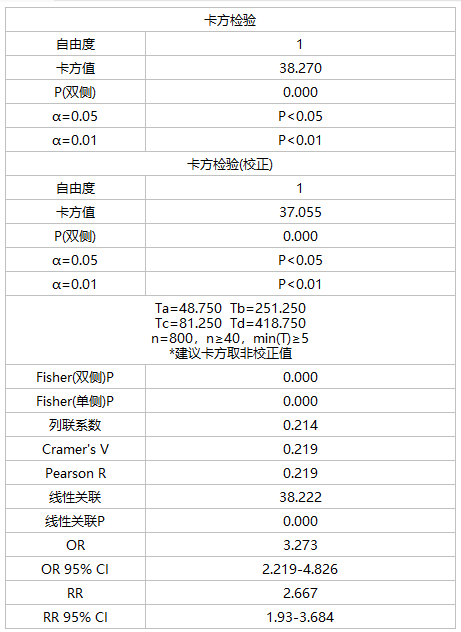
以下是一个关于吸烟与患肺癌的关系实例,展示了如何使用四格表卡方检验进行分析。研究对象是来自某地的300名吸烟者和500名非吸烟者。将它们整理成了一个四格表。表格如下所示:
| 患癌 | 未患癌 | 总数 | |
|---|---|---|---|
| 吸烟 | 80 | 220 | 300 |
| 不吸烟 | 50 | 450 | 500 |
| 总数 | 130 | 670 | 800 |
通过观察这个四格表,我们可以看到在吸烟患癌率比不吸烟患癌率高,但是这种观察不能证明吸烟与肺癌之间存在显著的关联。因此,需要使用四格表卡方检验来确定这种关联。
首先,需要计算每个单元格的期望值,即在假设吸烟与肺癌无关的情况下,每个单元格的预期人数。期望值计算公式为:期望值 = 行合计数 x 列合计数 / 样本总数。根据这个公式,计算得到期望值如下所示:
| 患癌 | 未患癌 | 总数 | |
|---|---|---|---|
| 吸烟 | 80 | 220 | 300 |
| 不吸烟 | 50 | 450 | 500 |
| 总数 | 130 | 670 | 800 |
符合N≥40 且T≥5,其中N为总样本量,T为最小期望值。可以使用四格表专用公式计算。
a=80,b=220,c=50,d=450,代入公式得卡方值等于38.27,自由度=(2-1)*(2-1)=1,查卡方界值表,P<0.01,这意味着,吸烟与肺癌之间存在显著的关联,也可以说吸烟与不吸烟存在显著性差异。具体来说,吸烟者的肺癌风险比非吸烟者高。这个结果表明,吸烟是肺癌的一个危险因素,可以用来指导肺癌的预防和治疗。
五、使用软件计算
可以使用SPSS计算卡方检验,但操作较为复杂,建议使用医学统计助手计算。