卡方检验(Chi-square test)是一种广泛用于分析分类数据之间关联性的统计检验方法。在医学领域,卡方检验经常用于分析不同治疗方法、疾病的发病情况与各种风险因素之间的关系。卡方检验分为多种类型,其中行乘列卡方检验是处理更复杂数据结构的有效方法。
一、行乘列卡方检验的特点
行乘列卡方检验是卡方检验的扩展形式,它主要用于分析两组以上变量之间的关系,适用于表格数据中行与列之间可能的相互作用。它的显著特点是能够处理更复杂的表格数据结构,而不仅仅局限于简单的2×2分类表。通过行乘列卡方检验,可以探讨不同类别之间的相互关系,并确定变量之间的依赖性。
二、行乘列格式卡方检验公式
1、卡方检验基本公式
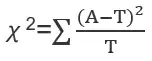
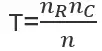
2、行乘列卡方检验专用公式
行乘列卡方检验时,要求不能有20%以上的单元格理论频数小于5,或者不能有任意一个单元格理论频数小于1,否则容易出现偏差。
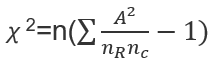
自由度df=(行数-1)(列数-1)
三、医学应用实例
在一个关于肿瘤治疗效果的临床研究中,研究人员评估了三种不同化疗方案对肺癌患者的治疗效果。根据患者的反应,将疗效分为“显著改善”、“无显著变化”和“恶化”。研究希望通过行乘列卡方检验,评估不同化疗方案对肺癌患者的疗效是否存在显著差异。
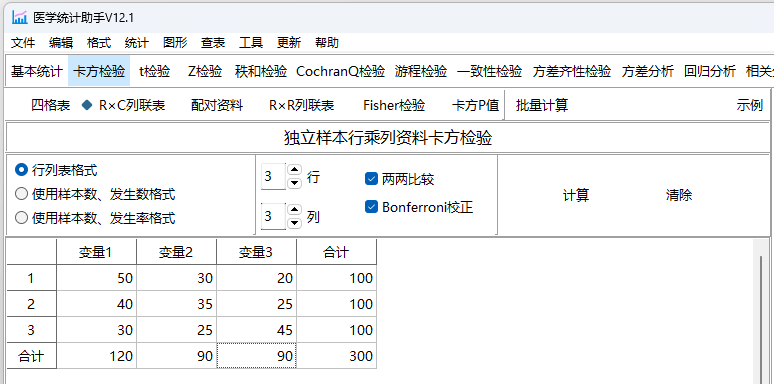
本研究共纳入了300名患者,分别采用了化疗方案A、化疗方案B和化疗方案C,治疗结果如下:
| 显著改善 | 无显著变化 | 恶化 | 合计 | |
|---|---|---|---|---|
| 化疗方案A | 50 | 30 | 20 | 100 |
| 化疗方案B | 40 | 35 | 25 | 100 |
| 化疗方案C | 30 | 25 | 45 | 100 |
| 合计 | 120 | 90 | 90 | 300 |
假设检验:
原假设(H0):三种化疗方案在治疗效果上没有显著差异。
备择假设(H1):三种化疗方案在治疗效果上存在显著差异。
依次计算期望值,得出下表:
| 显著改善 | 无显著变化 | 恶化 | 合计 | |
|---|---|---|---|---|
| 化疗方案A | 40 | 30 | 30 | 100 |
| 化疗方案B | 40 | 30 | 30 | 100 |
| 化疗方案C | 40 | 30 | 30 | 100 |
| 合计 | 120 | 90 | 90 | 300 |
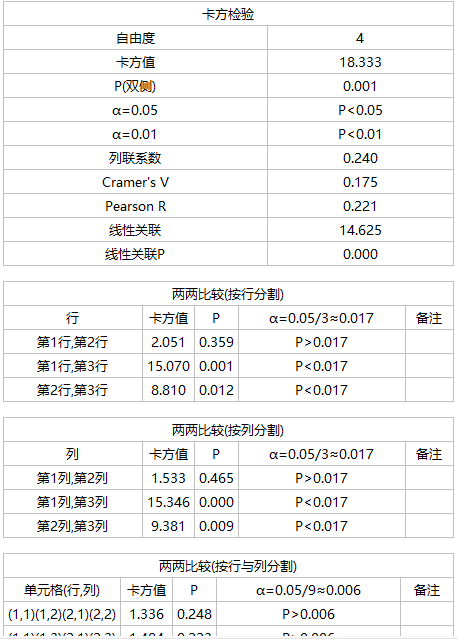
没有单元格理论频数小于5,也没有任意一个单元格理论频数小于1,所以可以使用行乘列专用公式计算,也可以使用卡方检验基本公式计算。将表中数据代入行乘列专用公式,得卡方值等于18.33,自由度=(3-1)*(3-1)=4,查卡方界值表得P<0.01,因此拒绝原假设,认为不同化疗方案在治疗效果上存在显著差异。
四、使用软件计算行乘列卡方检验
使用spss可以计算行乘列格式卡方检验,但操作较为复杂,建议使用医学统计助手进行计算。