方差分析是一种重要的统计方法,用于比较两个或多个样本均值之间的差异是否具有统计学意义。它能帮助研究人员对不同治疗方法、药物或者其他因素的影响进行量化分析,从而为临床决策提供有力的数据支持。
一、方差分析应用
1、单因素方差分析,例如,在某项研究中,科研人员可能需要评估三种不同药物治疗高血压的效果。通过使用单因素方差分析,研究人员可以确定这三种药物在降低血压方面是否存在显著差异。如果发现显著差异,可以进一步使用多重比较方法来确定哪些药物之间存在显著差异。
2、多因素方差分析可以用来评估两个或多个分类变量(如性别、年龄组、基因型等)对某一数值变量(如血压、血糖等)的影响。例如,研究人员可能想了解药物治疗和患者年龄对高血压患者血压降低效果的影响。通过使用两因素方差分析,研究人员可以同时考虑药物和年龄因素,评估它们的主效应以及相互作用效应。
3、研究对象可能在不同时间点接受多次测量。例如,在药物疗效观察研究中,患者可能在治疗前、治疗期间和治疗后的多个时间点接受血压测量。重复测量方差分析可以用来分析这种情况下的数据,评估时间效应、组间效应以及时间与组间的交互效应。
二、方差分析实例
随着医学研究的深入,药物疗效分析成为临床试验的重要组成部分。为了比较不同药物或治疗方法的疗效,研究者需要采用统计学方法,如方差分析,来确定观察到的差异是否具有统计学意义。以抗抑郁药物研究为例,展示了如何使用方差分析比较三种药物的疗效。
随机抽取了90名抑郁症患者,将他们分为三组,每组30人。分别使用药物A、药物B和药物C进行为期8周的治疗。研究的主要目的是比较三种药物在改善抑郁症状方面的效果。抑郁症状通过汉密尔顿抑郁量表(HAMD)评分来衡量,分数越低,抑郁症状越轻。
以下是实验结束后,各组患者的HAMD评分数据:
| 药物A组 | 药物B组 | 药物C组 |
| 28 | 19 | 10 |
| 21 | 12 | 7 |
| 25 | 15 | 6 |
| 19 | 9 | 5 |
| 32 | 22 | 15 |
| 27 | 17 | 8 |
| 24 | 14 | 7 |
| 30 | 20 | 12 |
| 23 | 13 | 8 |
| 20 | 10 | 6 |
| 18 | 8 | 5 |
| 31 | 21 | 11 |
| 29 | 19 | 9 |
| 22 | 12 | 6 |
| 26 | 16 | 8 |
| 33 | 23 | 13 |
| 19 | 9 | 5 |
| 24 | 14 | 7 |
| 28 | 18 | 11 |
| 17 | 7 | 4 |
| 21 | 11 | 6 |
| 29 | 19 | 10 |
| 27 | 17 | 9 |
| 31 | 21 | 11 |
| 20 | 10 | 5 |
| 22 | 12 | 7 |
| 25 | 15 | 8 |
| 33 | 23 | 13 |
| 30 | 20 | 12 |
| 23 | 13 | 8 |
计算方差分析:本例为完全随机设计资料的方差分析。
H0:三种药物疗效相同
H1:三种药物疗效不同
α<0.05
方差分析涉及三种不同的变异。
1、总变异,全部观测值大小不同,这种变异称为总变异。总变异的大小可以用离均差平方和表示,计算公式为:
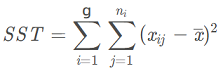
2、组间变异,各组由于接受处理因素的水平不同,各组的样本均数也大小不等,这种变异称为组间变异。计算公式为:
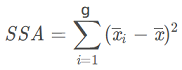
3、组内变异,在同一组中,虽然每个受试对象接受的处理因素水平相同,但观测值仍各不相同,这种变异称为组内变异(误差)。计算公式为:
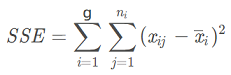
总离均差平方和(SST) = 组间离均差平方和(SSA) + 组内离均差平方和(SSE)
各离均差平方和的自由度为:
SST的自由度为n-1,n为观测值的个数;
SSA的自由度为g-1,g为因素水平的个数;
SSE的自由度为n-g。
总自由度(υ总)=组间自由度(υ组间)+组内自由度(υ组内)。
变异程度除与离均差平方和的大小有关外还与其自由度有关。由于各部分自由度不相等,所以各部分离均差平方和不能直接比较。须将各部分离均差平方和除以相应的自由度,其比值称为均方差,简称均方。
组间均方MSA=SSA/υ组间,组内均方MSE=SSE/υ组内。
组间均方与组内均方的比值称为F统计量,F=MSA/MSE,自由度υ1=υ组间=g-1,υ2=υ组内=n-g。
为方便计算,我们使用《医学统计助手》计算方差分析,医学统计助手软件是一款非常简单但功能强大的医学统计辅助工具,给出的计算结果也非常详细。
医学统计助手(www.statsas.com)
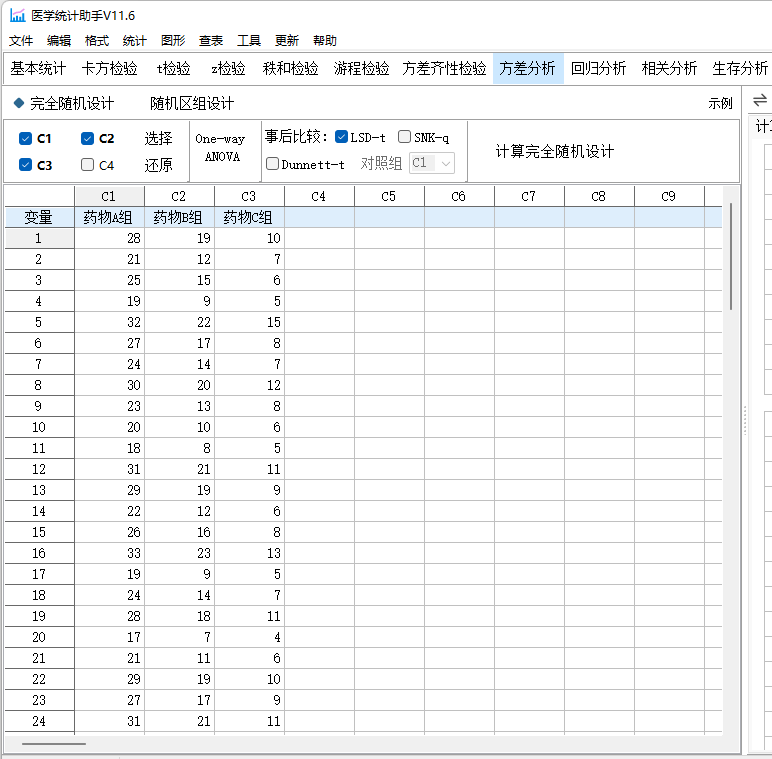
| 药物A组 | 药物B组 | 药物C组 | |
| 样本量 | 30 | 30 | 30 |
| 合计 | 757 | 459 | 252 |
| 最小值 | 17 | 7 | 4 |
| 最大值 | 33 | 23 | 15 |
| 平均数 | 25.2333 | 15.3 | 8.4 |
| 离均差平方和 | 651.3667 | 650.3 | 235.2 |
| 方差 | 22.4609 | 22.4241 | 8.1103 |
| 标准差 | 4.7393 | 4.7354 | 2.8479 |
| 观测值总数n | 90 |
| 因素水平个数g | 3 |
| 总合计ΣXij | 1468 |
| 总平均数 | 16.3111 |
| 组间离均差平方和SSA | 4296.4222 |
| 组内离均差平方和SSE | 1536.8667 |
| 组间均方MSA | 2148.2111 |
| 组内均方MSE | 17.6651 |
| 组间自由度(g-1) | 2 |
| 组内自由度(n-g) | 87 |
| F(2,87) | 121.6074 |
| p | 0 |
| α=0.05 | p<0.05 |
| α=0.01 | p<0.01 |
使用LSD-t检验,进行事后比较。
| 分组 | LSD-t | p | α=0.05 |
| 药物A组-药物B组 | 9.1534 | 0 | p<0.05 |
| 药物A组-药物C组 | 15.5116 | 0 | p<0.05 |
| 药物B组-药物A组 | -9.1534 | 0 | p<0.05 |
| 药物B组-药物C组 | 6.3582 | 0 | p<0.05 |
| 药物C组-药物A组 | -15.5116 | 0 | p<0.05 |
| 药物C组-药物B组 | -6.3582 | 0 | p<0.05 |
根据方差分析结果,F统计量为121.6074,对应的P值小于0.05。所以拒绝零假设(即三种药物疗效相同),认为三组间存在显著差异。通过进一步的多重比较(以LSD-t检验为例),可以确定这些差异主要存在于哪些药物之间。