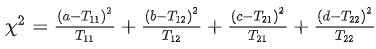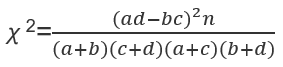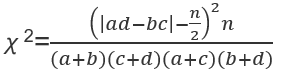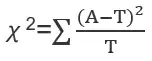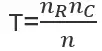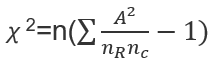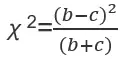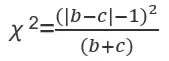最新版本：V12.1.2
发布日期：2024.10.10
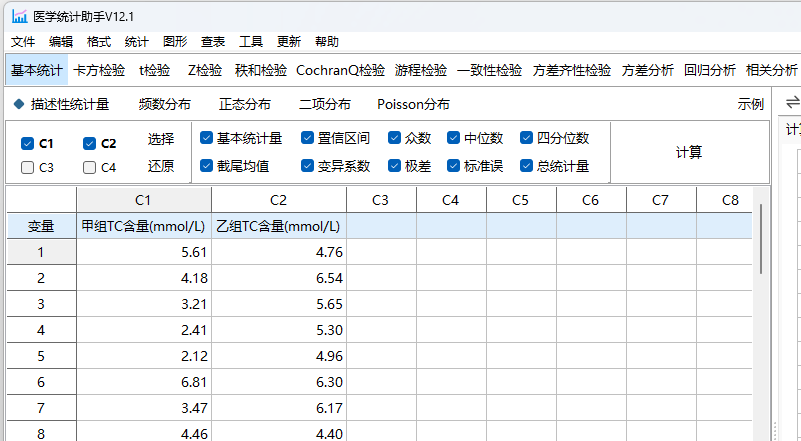
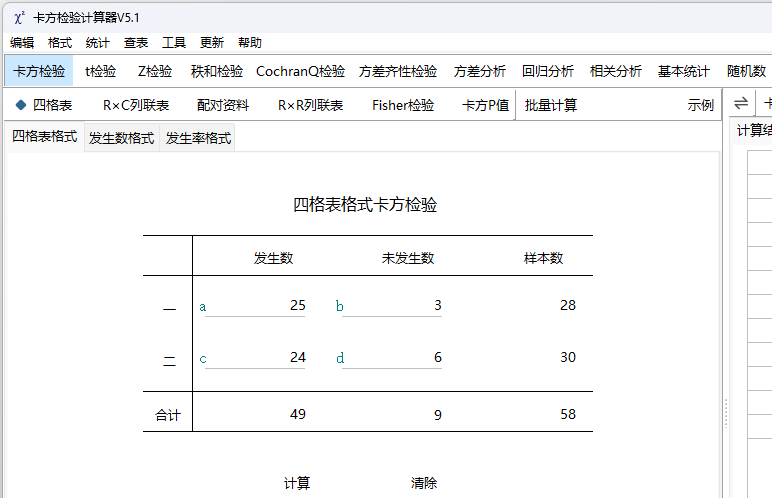
医学统计助手，是专为医学统计而设计的，简单易用。功能有基本统计、卡方检验、t检验、z检验、秩和检验、Cochran Q检验、游程检验、一致性检验、方差齐性检验、方差分析、回归分析、相关分析、生存分析、聚类分析、离散分布、样本量估算、随机数和统计图等实用功能。
一、软件特点
界面简洁，计算简便，直接输入数据点击计算就可以显示结果，没有大型统计软件的复杂操作，设计原则就是尽量减少操作步骤。体积小，速度快，无广告，无插件，无后门，注册后可断网使用，任何情况下不发送隐私信息。
二、软件安装
建议在各类软件管家中搜索”医学统计助手“直接安装，或查看下载与安装说明。
三、主要功能
（一）、基本统计：
1、描述性统计量；2、频数分布；3、正态分布；4、二项分布；5、Poisson分布。
最新版本：V5.1.2
发布日期：2024.10.10
在统计分析中卡方检验应用非常广泛，大型统计软件虽然功能强大，但操作相对复杂，而使用手工计算非常烦琐且易出错， 所以使用一款小巧的计算软件非常必要。卡方检验计算器是医学统计助手功能简化版，集成最常用统计检验功能，软件小巧实用，具有卡方检验、t检验、Z检验、秩和检验、Cochran Q检验、方差齐性检验、方差分析、回归分析、相关分析、基本统计和随机数等功能。
一、软件安装
建议在各类软件管家中搜索”卡方检验计算器“直接安装，或查看下载与安装说明。
（一）、卡方检验：
1、四格表卡方检验；2、行×列格式卡方检验；3、配对资料卡方检验；4、R×R列联表检验；5、Fisher精确检验；6、卡方p值；7、批量计算。
卡方检验应用于两个率或两个构成比比较；多个率或多个构成比比较以及分类资料的相关分析等。 分类为独立样本卡方检验和配对样本卡方检验，独立样本卡方检验包括四格表卡方检验和行乘列卡方检验， 配对样本卡方检验分为四格表形式的配对资料卡方检验和R×R列联表卡方检验。
一、四格表卡方检验
四格表卡方检验是卡方检验中最常使用的方法。四格表即2×2列联表，表内有ａ、ｂ、ｃ、ｄ４个基本数据，其余数据均由此４个数据推算出来的，故称为四格表资料。如下表。
| 组别 | 达标 | 未达标 | 合计 |
|---|---|---|---|
| 对照组 | a | b | a+b |
| 实验组 | c | d | c+d |
| 合计 | a+c | b+d | n |
1．基本公式
A表示实际频数，T表示理论频数。
计算过程：
𝑇𝑅𝐶 表示第R行第C列的理论(期望)频数，𝑛𝑅 表示第R行合计， 𝑛𝐶 表示第C列合计，n表示总合计。例如第一个单元格，为第1行第1列，实际频数a，理论频数
，同理
，
，
。
代入基本公式
自由度df=(行数-1)(列数-1)=(2-1)(2-1)=1
2．专用公式
N≥40 且最小理论频数T≥5
3．连续性矫正公式
N≥40 且最小理论频数1≤T＜5
4．n<40或最小理论频数T<1用Fisher精确检验，又叫确切概率检验
在计算小样本的P值时，不能根据卡方检验公式计算，可以使用Fisher精确检验直接计算出P值，Fihser精确检验只适用于计算小样本计数资料。
卡方检验（Chi-Square Test）是一种用于检验观察数据与理论预期之间差异是否显著的统计方法。在医学研究中，卡方检验特别适用于分析分类数据，例如疾病的发病率、治疗效果以及不同因素之间的关系。
一、卡方检验的原理
卡方检验用于判断观察到的频数与预期频数之间的差异是否显著。其基本假设是：观察到的分布与预期分布无显著差异，即变量之间没有关联。卡方统计量的基本公式为：
自由度df=(行数-1)(列数-1)
二、四格表（2×2表）的结构
卡方检验（Chi-square test）是一种广泛用于分析分类数据之间关联性的统计检验方法。在医学领域，卡方检验经常用于分析不同治疗方法、疾病的发病情况与各种风险因素之间的关系。卡方检验分为多种类型，其中行乘列卡方检验是处理更复杂数据结构的有效方法。
一、行乘列卡方检验的特点
行乘列卡方检验是卡方检验的扩展形式，它主要用于分析两组以上变量之间的关系，适用于表格数据中行与列之间可能的相互作用。它的显著特点是能够处理更复杂的表格数据结构，而不仅仅局限于简单的2×2分类表。通过行乘列卡方检验，可以探讨不同类别之间的相互关系，并确定变量之间的依赖性。
二、行乘列格式卡方检验公式
1、卡方检验基本公式
2、行乘列卡方检验专用公式
行乘列卡方检验时，要求不能有20%以上的单元格理论频数小于5，或者不能有任意一个单元格理论频数小于1，否则容易出现偏差。
配对资料也可以分为定量资料和定性资料，在定量资料中，如果数据符合正态分布的话，一般使用配对t检验，如果不符合正态分布，一般使用Wilcoxon符号秩和检验。在定性资料中，又可以分为配对2×2四格表资料和RxR列联表资料，配对2×2四格表资料一般应用McNemar卡方检验，RxR列联表资料一般应用Bowker卡方检验。
配对四格表资料卡方检验（McNemar检验）用于评估两种治疗方法在治疗某种疾病上的效果差异。
一、计算公式
1．b+c≥40
2．b+c<40，连续矫正公式
配对设计R*R的列联表资料（R>2）使用Bowker检验，当R=2时，等同于McNemar检验。 对于配对设计两分类资料，经典的方法是使用四格表的配对检验，也称McNemar检验。而对于配对设计多分类资料，可以使用Bowkor检验。该检验由A.H.Bowkor在1948年提出。Bowker检验也称平方表检验或对称检验，是McNemar检验的一般化及扩展。
一、Bowkor检验计算公式
自由度df=k(k-1)/2，如果有对称的两个单元格之和为0，则在公式中排除，自由度也相应的要减少。
正态分布，又称高斯分布，是自然界和社会科学中最常见的概率分布之一。许多统计方法和理论都依赖于数据的正态性假设，因此检验数据是否符合正态分布具有重要的意义。正态性检验是统计学中非常重要的一种检验方法，它用于检测数据是否符合正态分布。矩法正态性检验是一种常用的正态性检验方法。
一、矩法正态性检验原理
矩法正态性检验是利用数学上的矩原理来检验偏度（Skewness）和峰度（Kurtosis）。偏度反映了分布的不对称程度和方向，用偏度系数衡量，样本偏度系数用g1表示，总体偏度系数用γ1表示。峰度反映了与正态曲线相比的冒尖程度和扁平程度，用峰度系数衡量，样本峰度系数用g2表示，总体峰度系数用γ2表示。理论上，总体偏度系数γ1=0为对称，γ1>0为正偏态，γ1<0为负偏态；总体峰度系数γ2=0为正态峰，γ2>0为尖峭峰，γ2<0为平阔峰。只有同时满足对称和正态峰两个条件时，才能认为资料服从正态分布。
偏度系数：描述数据分布不对称的方向及其程度，如图
