在医学统计中,相关分析是一种常用的方法,用于研究两个或多个变量之间的关系。使用相关分析可发现变量之间的线性或非线性关系,为后续的实验设计、临床研究和治疗策略提供依据。
常用相关分析方法有:
1.皮尔逊相关分析(Pearson Correlation),用于衡量两个连续变量之间的线性关系。皮尔逊相关系数(r)的取值范围为-1至1。r=1表示完全正相关,r=-1表示完全负相关,r=0表示无相关。
2.斯皮尔曼等级相关分析(Spearman Rank Correlation),用于衡量两个变量之间的单调关系,主要用于非线性关系或非正态分布数据。它通过计算原始数据的等级差异来评估关系,因此对异常值和数据分布较为稳健。
3.肯德尔等级相关分析(Spearman Rank Correlation),与斯皮尔曼等级相关分析类似,也是用于衡量两个变量之间的单调关系。它基于变量之间的配对观测值的一致性或不一致性来计算相关性。相对于斯皮尔曼相关,肯德尔相关对异常值更为稳健。
相关分析应用举例:
1.生物标志物与疾病风险:使用相关分析来研究生物标志物(如血压、血脂水平、血糖水平等)与特定疾病风险之间的关系,从而确定潜在的危险因素和预测疾病发生的可能性。
2.临床试验中的治疗效果:在临床试验中,使用相关分析可以评估治疗方法对多个变量(如生理指标、症状、生活质量等)的影响,从而确定最有效的治疗策略。
3.环境因素与健康状况:通过相关分析,评估环境因素(如空气污染、水质、生活方式等)与健康状况之间的关系,从而为预防措施和公共卫生政策提供依据。
4.风险因素与预后:在疾病管理中,相关分析可以用于探讨不同风险因素(如年龄、性别、疾病历程等)与患者预后(如生存率、复发率、并发症等)之间的关系,从而指导临床决策和患者随访。
以皮尔逊相关分析为例:
假设研究肥胖与血糖水平之间的关系,选取体重指数(BMI)与空腹血糖水平(FBG)做相关分析。以下是20名成年人的数据(数值仅作示例):
| 编号 | BMI | FBG (mmol/L) |
|---|---|---|
| 1 | 21.2 | 4.56 |
| 2 | 23.1 | |
| 3 | 26.8 | 5.67 |
| 4 | 28.9 | 6.50 |
| 5 | 24.7 | 4.83 |
| 6 | 33.1 | 7.67 |
| 7 | 20.9 | 4.17 |
| 8 | 29.8 | 6.72 |
| 9 | 26.3 | 5.50 |
| 10 | 27.4 | 5.83 |
| 11 | 25.1 | 5.06 |
| 12 | 24.2 | 4.72 |
| 13 | 22.7 | 4.56 |
| 14 | 30.2 | 6.83 |
| 15 | 28.1 | 6.11 |
| 16 | 22.4 | 4.56 |
| 17 | 27.9 | 6.44 |
| 18 | 24.5 | 4.94 |
| 19 | 33.8 | 8.22 |
| 20 | 26.9 | 5.44 |
使用皮尔逊相关分析来计算BMI与FBG之间的相关系数。计算公式为:
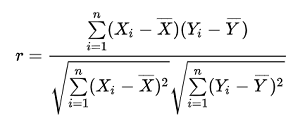
为了计算简便,选择使用医学统计助手进行计算相关分析。
医学统计助手(statsas.com)

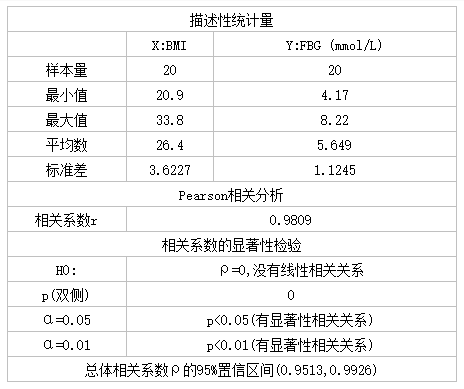
经过计算相关系数r=0.9809,显著性检验,p<0.01,所以BMI与FBG之间存在很强的正相关关系。这表明BMI值越高,血糖水平也越高。
需要注意的是,皮尔逊相关分析只能检测线性关系,而且相关性并不意味着因果关系。在研究肥胖与血糖之间的关系时,还需要考虑其他潜在因素,如饮食、运动、药物使用等。此外,BMI值并不能完全反映个体的体脂肪分布和代谢情况,因此在研究肥胖与疾病风险时,应结合其他测量指标,如腰围、腰臀比、体脂肪含量等。在进行相关分析时,还需要注意数据的分布特征、异常值和潜在的混杂因素,以确保结果的可靠性和有效性。