秩和检验是一种常用的非参数假设检验方法,用于比较两个或多个独立或配对样本的中位数是否相等。在医学研究中,秩和检验常用于比较不同治疗方案或条件的效果差异,特别是在数据不满足正态分布假设的情况下。
一、配对样本秩和检验
配对资料秩和检验是一种常用的非参数假设检验方法,用于比较同一组体验受到两种不同治疗方案或条件的影响。在医学研究中,配对资料秩和检验常用于比较某种治疗前后的效果差异。
比较两种不同的药物治疗方案对糖尿病患者血糖控制的影响。随机抽取20名患者,每个患者在使用药物A和药物B治疗时,血糖控制指标进行评估。以下是每个患者在两种治疗方案下的血糖控制指标数据:
| 患者编号 | 药物A血糖控制指标 | 药物B血糖控制指标 | 配对差值 | 秩 |
|---|---|---|---|---|
| 1 | 7.1 | 6.8 | 0.3 | 15 |
| 2 | 8.5 | 8.1 | 0.4 | 20 |
| 3 | 7.6 | 7.7 | -0.1 | -2.5 |
| 4 | 6.8 | 6.5 | 0.3 | 15 |
| 5 | 9.2 | 8.9 | 0.3 | 15 |
| 6 | 7.9 | 8.1 | -0.2 | -7.5 |
| 7 | 8.3 | 8.6 | -0.3 | -15 |
| 8 | 6.9 | 6.7 | 0.2 | 7.5 |
| 9 | 7.8 | 7.9 | -0.1 | -2.5 |
| 10 | 8.6 | 8.9 | -0.3 | -15 |
| 11 | 9 | 9.2 | -0.2 | -7.5 |
| 12 | 6.5 | 6.7 | -0.2 | -7.5 |
| 13 | 8.1 | 7.8 | 0.3 | 15 |
| 14 | 7.4 | 7.7 | -0.3 | -15 |
| 15 | 7.7 | 7.8 | -0.1 | -2.5 |
| 16 | 6.2 | 6.5 | -0.3 | -15 |
| 17 | 9.3 | 9.6 | -0.3 | -15 |
| 18 | 8.4 | 8.6 | -0.2 | -7.5 |
| 19 | 6.7 | 6.8 | -0.1 | -2.5 |
| 20 | 7.2 | 7.4 | -0.2 | -7.5 |
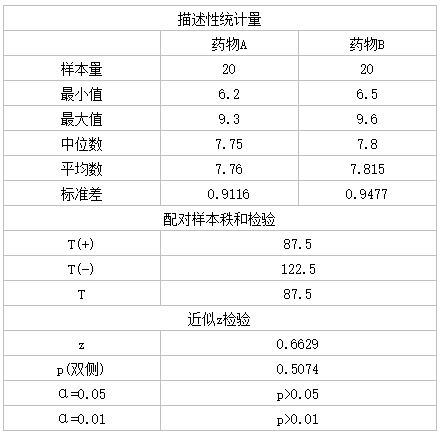
H0:差值的总体中位数Md=0
H1:Md≠0
α=0.05
求检验统计量T值:首先按差值的绝对值从小到大编秩次,再让秩次保持原差值的正负号。编秩次时:1.舍去差值为0的对子数,同时样本例数相应减少。2.遇到绝对值相等时取平均秩次。3.任取正秩和或负秩和为T。
求p值:当n≤50时可以查T值界值表,找到左侧n,将检验统计量T值与相邻左侧一栏的界值相比,若T在上下界范围内,其p值大于表上方相应概率水平,若T值在上下界值范围外,其p值小于相应概率水平,可向右移一栏,再与界值相比。
若n>50,超出界值表范围,可用正态近似法作z检验。 由于计算复杂建议使用软件计算秩和检验。
医学统计助手(statsas.com)

二、独立样本秩和检验
独立样本秩和检验是一种常用的非参数假设检验方法,用于比较两个独立样本的中位数是否相等。在医学研究中,独立样本秩和检验常用于比较两种不同治疗方案或条件的效果差异。
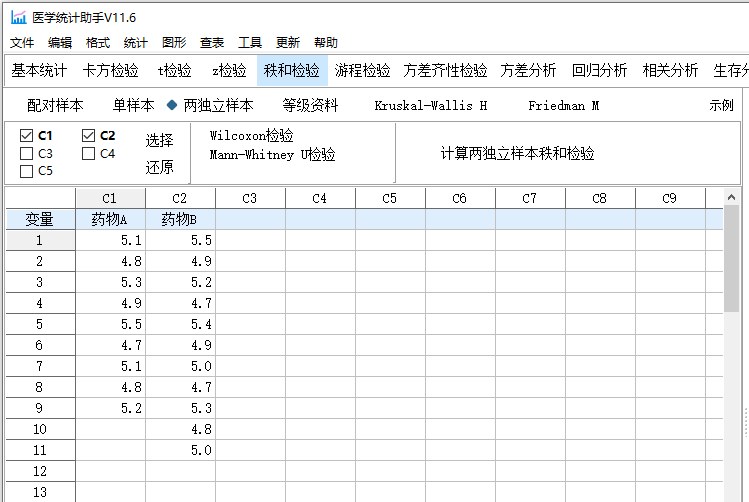
该研究比较两种不同的药物对肌肉疼痛的缓解效果。随机抽取20名患者,9名患者接受了药物A,另外11名患者接受了药物B。以下是两组患者的疼痛程度评分:
| 药物A | 药物B |
|---|---|
| 5.1 | 5.5 |
| 4.8 | 4.9 |
| 5.3 | 5.2 |
| 4.9 | 4.7 |
| 5.5 | 5.4 |
| 4.7 | 4.9 |
| 5.1 | 5.0 |
| 4.8 | 4.7 |
| 5.2 | 5.3 |
| 4.8 | |
| 5.0 |
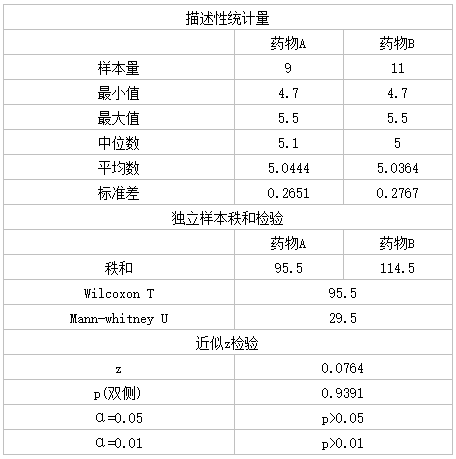
比较两种药物对肌肉疼痛的缓解效果是否显著不同。
计算结果如下:
三、两个独立样本等级资料秩和检验
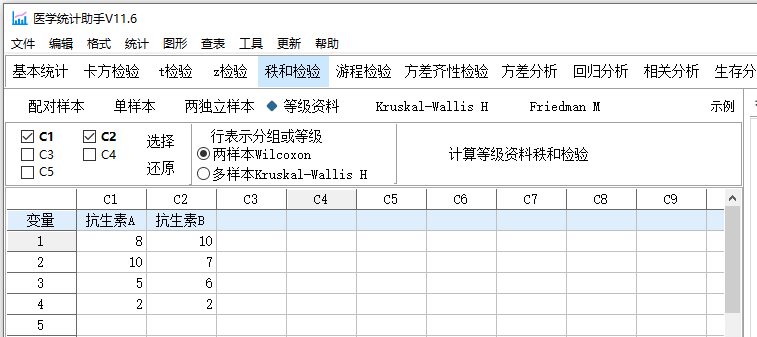
比较了两种不同的抗生素治疗方案对肺炎患者的治疗效果。研究了50名患者,其中25名患者接受了抗生素A,另外25名患者接受了抗生素B。在治疗结束时,研究人员对参与者进行了肺炎症状的主观评估,结果用4个等级进行了评估,分别为0、1、2和3,其中0表示症状最轻,3表示症状最重。以下是两组患者的主观症状等级分布频数表:
| 疗效等级 | 抗生素A | 抗生素B |
|---|---|---|
| 0 | 8 | 10 |
| 1 | 10 | 7 |
| 2 | 5 | 6 |
| 3 | 2 | 2 |
计算结果如下:
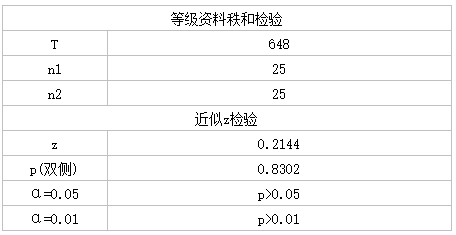
多样本秩和检验计算方法与以上方法类似,方法为完全随机设计Kruskal-Wallis H秩和检验;随机区组设计Friedman M秩和检验。可用使用医学统计助手进行计算,使用都十分方便。
秩和检验不能替代正态分布假设的t检验,而是作为其一种非参数替代方法。在数据满足正态分布的情况下,使用t检验可以获得更高的检验效能。