统计学习

卡方检验（Chi-Square Test）是一种用于检验观察数据与理论预期之间差异是否显著的统计方法。在医学研究中，卡方检验特别适用于分析分类数据，例如疾病的发病率、治疗效果以及不同因素之间的关系。

一、卡方检验的原理

卡方检验用于判断观察到的频数与预期频数之间的差异是否显著。其基本假设是：观察到的分布与预期分布无显著差异，即变量之间没有关联。卡方统计量的基本公式为：

自由度df=(行数-1)(列数-1)

二、四格表（2×2表）的结构

阅读更多

卡方检验（Chi-square test）是一种广泛用于分析分类数据之间关联性的统计检验方法。在医学领域，卡方检验经常用于分析不同治疗方法、疾病的发病情况与各种风险因素之间的关系。卡方检验分为多种类型，其中行乘列卡方检验是处理更复杂数据结构的有效方法。

一、行乘列卡方检验的特点

行乘列卡方检验是卡方检验的扩展形式，它主要用于分析两组以上变量之间的关系，适用于表格数据中行与列之间可能的相互作用。它的显著特点是能够处理更复杂的表格数据结构，而不仅仅局限于简单的2×2分类表。通过行乘列卡方检验，可以探讨不同类别之间的相互关系，并确定变量之间的依赖性。

二、行乘列格式卡方检验公式
1、卡方检验基本公式

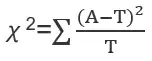
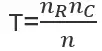
2、行乘列卡方检验专用公式

行乘列卡方检验时，要求不能有20%以上的单元格理论频数小于5，或者不能有任意一个单元格理论频数小于1，否则容易出现偏差。

阅读更多

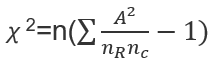
配对资料也可以分为定量资料和定性资料，在定量资料中，如果数据符合正态分布的话，一般使用配对t检验，如果不符合正态分布，一般使用Wilcoxon符号秩和检验。在定性资料中，又可以分为配对2×2四格表资料和RxR列联表资料，配对2×2四格表资料一般应用McNemar卡方检验，RxR列联表资料一般应用Bowker卡方检验。

配对四格表资料卡方检验（McNemar检验）用于评估两种治疗方法在治疗某种疾病上的效果差异。

一、计算公式

1．b+c≥40

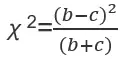
2．b+c<40，连续矫正公式

阅读更多

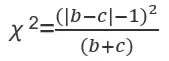
配对设计R*R的列联表资料（R>2）使用Bowker检验，当R=2时，等同于McNemar检验。 对于配对设计两分类资料，经典的方法是使用四格表的配对检验，也称McNemar检验。而对于配对设计多分类资料，可以使用Bowkor检验。该检验由A.H.Bowkor在1948年提出。Bowker检验也称平方表检验或对称检验，是McNemar检验的一般化及扩展。

一、Bowkor检验计算公式

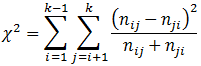
自由度df=k(k-1)/2，如果有对称的两个单元格之和为0，则在公式中排除，自由度也相应的要减少。

阅读更多

正态分布，又称高斯分布，是自然界和社会科学中最常见的概率分布之一。许多统计方法和理论都依赖于数据的正态性假设，因此检验数据是否符合正态分布具有重要的意义。正态性检验是统计学中非常重要的一种检验方法，它用于检测数据是否符合正态分布。矩法正态性检验是一种常用的正态性检验方法。
一、矩法正态性检验原理
矩法正态性检验是利用数学上的矩原理来检验偏度（Skewness）和峰度（Kurtosis）。偏度反映了分布的不对称程度和方向，用偏度系数衡量，样本偏度系数用g1表示，总体偏度系数用γ1表示。峰度反映了与正态曲线相比的冒尖程度和扁平程度，用峰度系数衡量，样本峰度系数用g2表示，总体峰度系数用γ2表示。理论上，总体偏度系数γ1=0为对称，γ1>0为正偏态，γ1<0为负偏态；总体峰度系数γ2=0为正态峰，γ2>0为尖峭峰，γ2<0为平阔峰。只有同时满足对称和正态峰两个条件时，才能认为资料服从正态分布。

偏度系数：描述数据分布不对称的方向及其程度，如图

阅读更多

游程检验是一种统计方法，用于检测数据序列中的随机性。在许多领域，如金融、气象学、生物学和社会科学等，都需要评估观测数据是否具有随机性。随机性是许多领域研究的基础。对数据序列的随机性进行检验有助于判断数据是否受到某种系统性影响，或者是否具有某种潜在的模式。游程检验是一种常用的随机性检验方法，其基本思想是分析数据序列中连续相同值的子序列的长度（即游程），以判断整个序列是否具有随机性。

一、游程检验在医学统计中的应用：

在医学统计中，评估数据序列的随机性具有重要意义。通过检验数据的随机性，可以判断实验结果是否受到某种系统性误差的影响，以及评估患者生理信号的稳定性和异常。例如实验设计、生物信号分析、疫情分析等等方面。

阅读更多

Cochran Q检验是一种非参数统计方法，用于比较三个或更多相关样本中的二分类变量（如成功/失败、通过/未通过等）的比例。Cochran Q检验是Friedman检验在二分类情况下的特殊情况，它主要应用于重复测量设计或随机区组设计。Cochran Q检验旨在检测在不同条件下，受试者的二分类响应是否存在显著差异。

假设对比三种不同的止痛药对慢性头痛患者缓解症状的效果。随机选择了20名诊断为慢性头痛的患者。为了比较三种止痛药的效果，将每个患者分配到三个阶段的治疗，每个阶段为2周，中间有一个为期2周的洗脱期。三种止痛药包括：止痛药A、止痛药B、止痛药C。在每个阶段结束时，记录患者的头痛症状是否得到有效缓解(成功或失败)。1表示成功，0表示失败。表格中是收集到的数据。

为了确定三种止痛药的疗效有无显著性差异，可以使用Cochran Q检验计算Q值和P值。如果P值小于预先设定的显著性水平(例如0.05)，就可以拒绝H0(所有止痛药的疗效相同)，并得出结论：至少有一种止痛药的疗效与其他止痛药不同。

医学统计助手(www.statsas.com)

阅读更多

卡方检验（chi-squared test）是用于比较观察数据和期望数据之间的差异是否显著的一种统计方法。在进行卡方检验时，需要计算卡方统计量和p值，并将这些结果与显著性水平进行比较，来判断差异是否具有统计学意义。

卡方检验结果通常包括卡方统计量、自由度和显著性水平（P值）：

1. 卡方统计量：卡方统计量（chi-square statistic）是用于衡量观察数据和期望数据之间差异的量。卡方统计量的计算方式为，将每个观察值与对应的期望值之间的差异平方后除以期望值，然后将这些值加总。卡方统计量越大，表示观察数据与期望数据之间的差异越大。在进行卡方检验时，一般会计算卡方统计量，并将其与自由度一起用于查找卡方分布表以获取p值。
2. 自由度：自由度（degrees of freedom）指的是进行卡方检验时可以自由变化的参数个数。在卡方检验中，自由度的计算方法为，自由度 = (行数 – 1) x (列数 – 1)。例如，如果进行2×2的卡方检验，则自由度为1。
3. p值：p值（p-value）是用于判断差异是否具有统计学意义的重要指标。一般来说，P 值小于预先设定的显著性水平（如 0.05 或 0.01），则认为观察到的差异是显著的，拒绝零假设，认为观察数据和期望数据之间的差异具有统计学意义。反之，如果 P 值大于显著性水平，无法拒绝零假设，即观察到的差异可能是偶然产生的，认为观察数据和期望数据之间的差异不具有统计学意义。

阅读更多