Fisher精确检验是一种在统计分析中经常使用的方法,旨在评估两个分类变量之间是否存在显著关系。这种方法由罗纳德·A·费舍尔(Ronald A. Fisher)于20世纪20年代提出,并被广泛应用于小样本数据集的分析。与卡方检验相比,Fisher精确检验在处理低频观察值(如小于5)的情况下更为精确,因为卡方检验在这种情况下可能导致误差。
Fisher精确检验的基本原理是利用超几何分布计算观察数据出现的概率。它通常用于处理2×2列联表,这种表格包含两个分类变量,每个变量有两个水平。通过对比观察数据与随机分布数据之间的差异,可以判断两个分类变量之间是否存在显著关联。
当计算卡方检验时遇到n<40或T<1,或得到的概率P≈α时,需使用Fisher精确检验。
以下是Fisher精确检验的操作步骤:
- 构建一个2×2列联表,填入观察到的频数。
- 计算表格中每个单元格的期望频数。
- 利用超几何分布计算观察数据出现的概率,即P值。
- 将计算出的P值与预定的显著性水平(如0.05)进行比较。
- 若P值小于或等于显著性水平,可以拒绝原假设,认为两个分类变量之间存在显著关联。反之,若无法拒绝原假设,则表明没有足够证据支持两个变量之间的关联。
假设要进行一项医学研究,探讨吸烟是否是某种罕见疾病的风险因素。我们收集了一组小样本数据,包括吸烟者和非吸烟者。以下是研究结果:
| 患病 | 未患病 | 总数 | |
|---|---|---|---|
| 吸烟者 | 5 | 8 | 13 |
| 非吸烟者 | 1 | 6 | 7 |
| 总数 | 6 | 14 | 20 |
H0:吸烟与该罕见疾病之间不存在显著关联
H1:吸烟与该罕见疾病之间存在显著关联
α=0.05
手工计算太复杂,建议使用软件进行计算,以医学统计助手为例
医学统计助手(statsas.com)
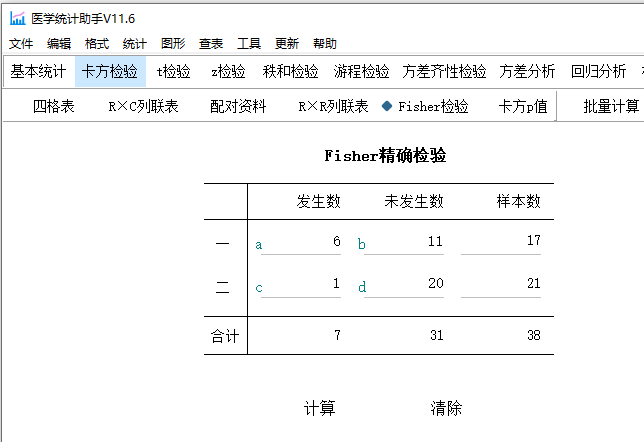

计算得p=0.0313,小于显著性水平(α=0.05),因此拒绝原假设,认为吸烟与该罕见疾病之间存在显著关联。也就是,吸烟可能是该罕见疾病的一个风险因素。
Fisher精确检验的一个显著优势是其在小样本数据集中提供较为准确且可靠的结果。然而,这种方法的计算复杂度较高,特别是在大样本或更高维度的列联表中。在这些情况下,通常会倾向于使用卡方检验或其他替代方法。