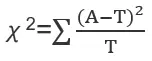四格表卡方检验是医学统计学中常用的一种方法,用于确定两个分类变量之间是否存在关联。在医学研究中,四格表卡方检验被广泛应用于研究疾病和治疗方法之间的关联,以及预测疾病发展的风险因素。
四格表卡方检验基于一个二维表格,也称为四格表。表格中的行和列分别代表两个分类变量。例如,行可以代表男性和女性,列可以代表吸烟和不吸烟。表格中的每个单元格代表两个变量的交叉部分,例如男性吸烟者的数量。四格表卡方检验的目的是确定这些变量之间是否存在关联,如果存在关联,则表示两个变量之间有统计学上的显著性关系。
四格表卡方检验的原理是基于比较实际观察值和期望值之间的差异。实际观察值是指在样本中观察到的数据,而期望值是指在假设无关联的情况下,预计会发生的数据。通过比较实际观察值和期望值,可以计算出卡方值,该值越大表示观察到的数据与假设无关联的期望数据之间的差异越大。